| 3.9 Amplitude corrections | ||
|---|---|---|
| Chapter 3. Audio | | |
At the end of this large chapter devoted to audio techniques in Pd, we'll now take a look at amplitude processing.
As you learned in 3.1.2.1.2, the loudspeaker membrane can only vibrate up to a certain point; thereafter it is simply "clipped". You can, however, build an automatic device that reduces parts of a signal that are too loud before they clip. In acoustic engineering, a device that accomplishes this task is called a "limiter".
With a limiter, there is only one input signal whose volume has to be measured. If it exceeds the set upper limit, its volume will be reduced according to a set factor until it reaches the reference point. (In the following section, volume is calculated in dB.)
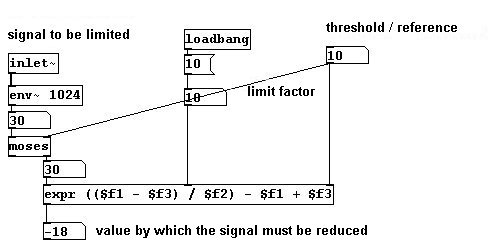
In the first example, the threshold is 10 dB, the factor 10, and the input signal 30 dB. The difference between the input signal and the reference point is 20 dB. The factor determines that it should be reduced (by a factor of 10) to 2 dB; i.e. the input signal must be reduced by -18 dB to a value of 12 dB.
Now we'll apply the limiting factor to the original signal whenever it exceeds the threshold; if it stays below the threshold, the factor simply remains 1:
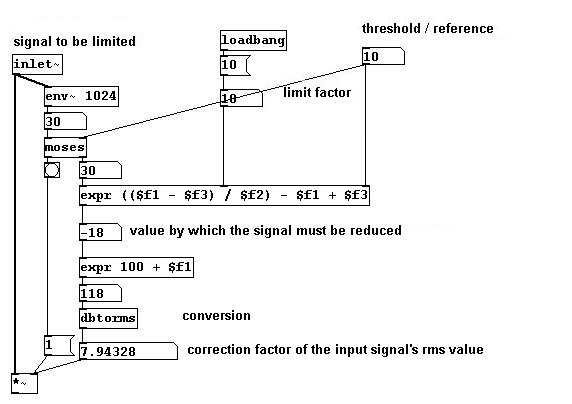
There are two aspects at work: "env~" takes the average within the given sample, here always in a window of 1024 samples. That results in a delay of 1024 / 44.1 = 23.22 milliseconds that you can set. But you could also perform the reduction before the signal exceeds the threshold, which would delay the original signal even more. In signal processing, the term for this is "feedforward control action". If the delay of the original signal is shorter and the delay of the correction longer, one speaks of "reverse control action". In this case, the threshold is exceeded briefly before any correction is made. Some variables that have to be defined here are the speed at which the correction occurs and also the speed with which the signal returns to its original volume once it falls below the threshold again; these are called "attack" and "release" times.
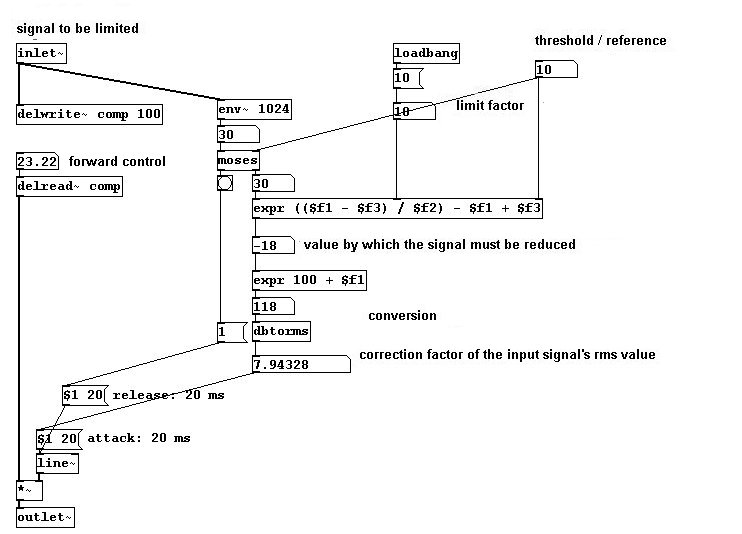
Once you've established the upper threshold (after which correction occurs) and the reference point (the point that corrections approach), you can also adjust the settings so that volumes below the reference point are amplified and those above it are made quieter. A device that accomplishes this task is called a compressor:
If you connect a microphone input to a speaker - e.g., the "adc~" object directly to the "dac~" - and hold the microphone to the speaker, you'll soon hear a tone (and you'd best point the microphone away fast!). This is because air always contains some noise; the microphone picks it up and sends it to the speaker; the speaker plays it and the microphone picks up this amplified signal; etc. Depending on the distance between the microphone and the speaker, the signal is amplified each time. Depending on the room, cable length, and latency in the computer, this results in different high periodic tones, also called "Larsen Tones". At the same time, volume increases dramatically, as the signal is constantly being amplified. This is the classic case of feedback - a circuit, a recursive system. Wherever microphones and speakers are used, there is a danger of feedback. A limiter used between the microphone and the speaker could help allay this danger.
Volume can be used to simulate movement in space. Normally we have a pair of stereo speakers and therefore two inputs for "dac~". If you change the relative volumes of the speakers gradually - provided you are directly between the two speakers - you can experience how sound 'travels' back and forth between the two speakers. This is called a 'phantom sound source'.
patches/3-9-3-1-spatial-stereo.pd
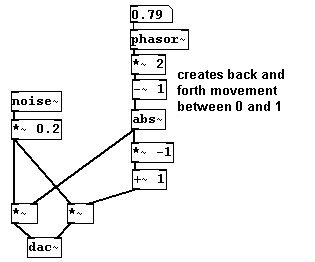
Speaker set-up:

If you have, say, four speakers set up in a square, you can create circular movement through space (naturally, this requires a sound card with four separate outputs; as arguments, you can give the inputs to the "dac~"):
patches/3-9-3-1-spatial-quadro.pd
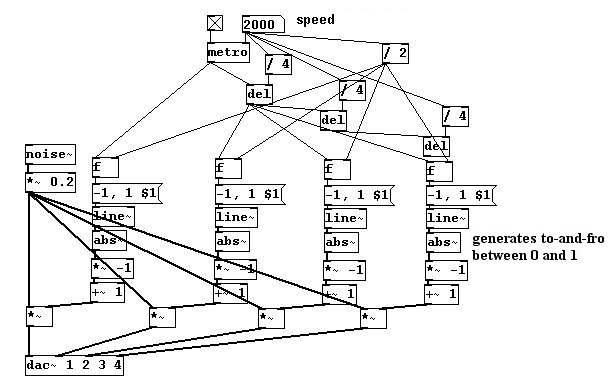
Set-up:
In this case as well, the effect only works correctly if you are precisely in the middle (in the "sweet spot"). In the above example, you can also clearly hear a 'hole' in the volume between the two highest volume levels for each speaker. You should experiment to see whether the overlapping of the volume should be linear or exponential (cf. the window types in 3.9.4). The composer has to use her ear and decide for herself.
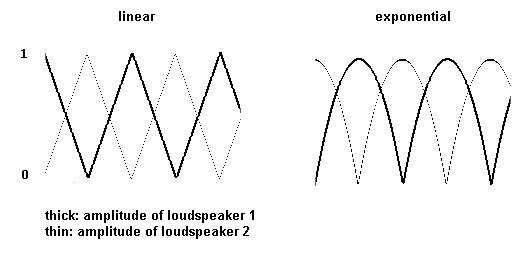
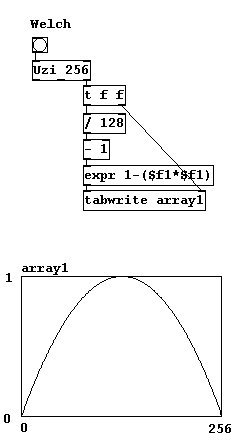
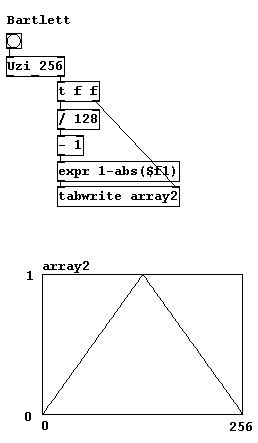
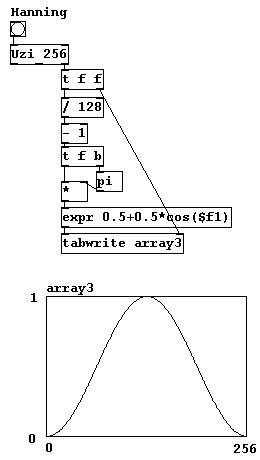
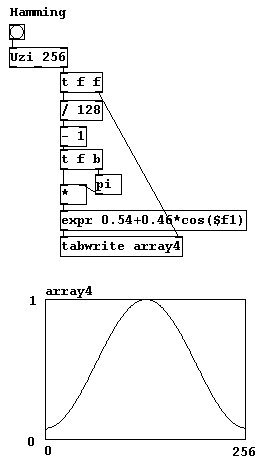
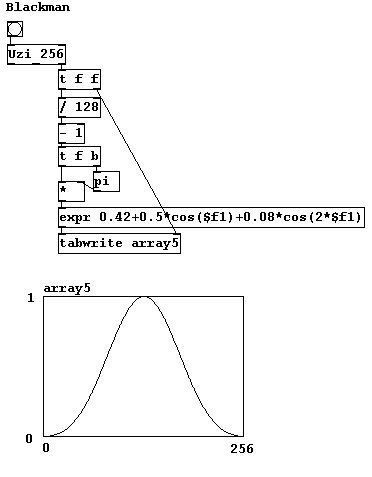
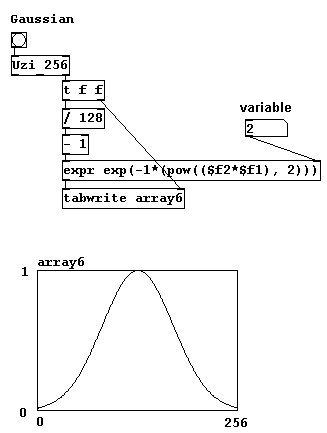
In previous chapters, "Hanning" windows (which correspond to part of a cosine function) were often used to avoid clicks. But there are also other types of windows that you could experiment with: