Algorithm is the technical term for the description of a sequence of steps in a procedure that a computer program executes.

If you have a subpatch that adds 1 to an entered number, you could already consider this a (very simple) algorithm: this subpatch's algorithm is the addition of 1.

patches/4-1-1-1-plus-one-algorithm.pd

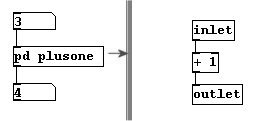
In essence, every object in Pd executes an algorithm. What used to require the use of a device called a noise generator is accomplished today with the algorithm contained in the "noise~" object.

In this chapter, we are particularly interested in developing algorithms that, once we initiate processing, the computer can execute completely on its own and that fulfill the purpose of changing sound in time. Some examples of this have been named already, like in 2.2.3.2.7

A very simple but abundant way to get the computer to operate on its own is by using a random generator.

patches/4-1-2-1-random.pd

You can apply limits to this random selection that themselves change:

patches/4-1-2-1-random-limits.pd

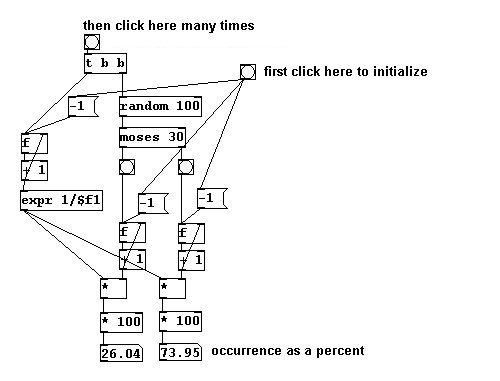
The result of a random generator follows the laws of stochastics, that is, of probability. With "random 6", every number from 0 to 5 has a probability of 1/6. Though highly improbable, it is possible that one of the numbers would never appear or wouldn't appear for a very long time. This probability can also be directly controlled:

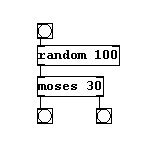
Here, the probability that a bang occurs on the left is 30 percent and 70 percent on the right. You can test this as shown here:

patches/4-1-2-1-probability.pd

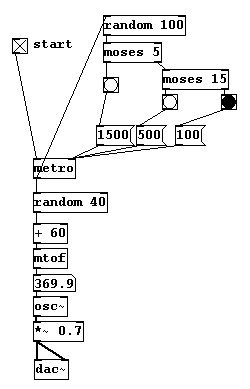
You can use this principle to select different durations for certain sound events: short occur very frequently, medium once in a while, and long rarely.

patches/4-1-2-1-probability-examples.pd

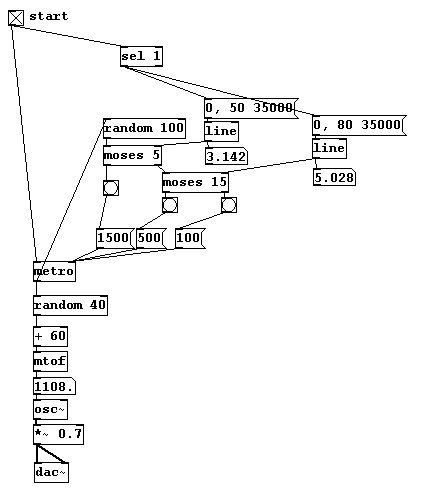
You could also invert this distribution over time...

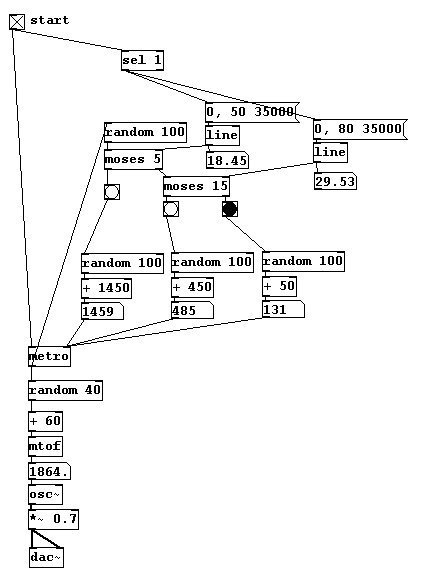
At the beginning there are only short durations, at the end mainly long ones (which naturally require a lot of time).

Also, a little bit of variation can be introduced to the different durations:

You can keep going with this, of course, 'randomizing' more and more parameters in your patch as you see fit.

There is a piece by Alvin Lucier based on a relatively simple idea: someone sits in a room and speaks into a microphone. This speech is recorded and then played back in the room. This playback is in turn recorded, played back, re-recorded, and so forth. Each time, the quality of the recording is worse, more and more information is lost. More specifically, the frequencies that the loudspeaker, microphone, and room can represent well are propagated while the others are gradually filtered out.

This can be easily programmed in Pd:

patches/4-1-2-2-lucier.pd

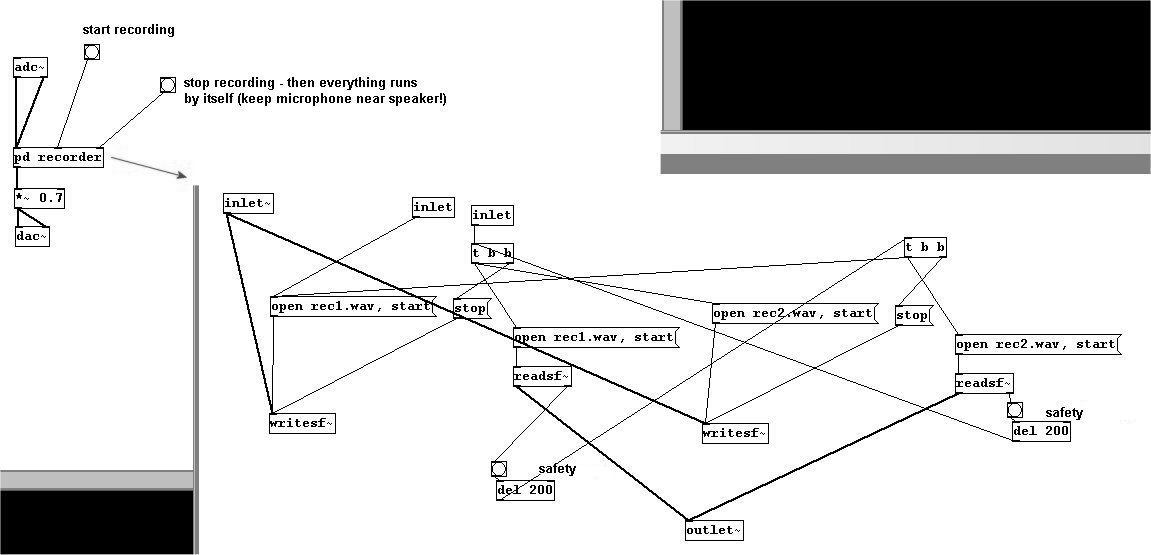
You could say that the algorithm is recording and playback. In this case, the result is fed back into the algorithm again and again. A process that runs automatically in this way is called a recursion. Recursions have already been mentioned in 3.4.2.9 and 3.4.2.10.

In the next example, we will also use alteration and re-recording. A recursive ring modulation:

Recursions that work purely with numbers can also be interesting. One of the most well known examples of this that frequently occurs in music is the Fibonacci series. The algorithm is that the last two numbers in a list are added together to produce a new final result in the list.

patches/4-1-2-3-fibonacci.pd

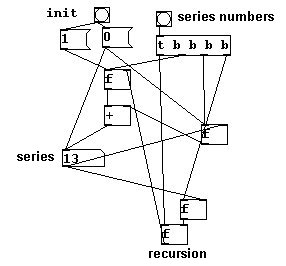
a) Record a sample and play it back at the wrong speed. Record this 'wrong' playback, play it back, record, and so forth. Try this while (1) playing back the sample with the same 'wrong' speed and (2) with a different 'wrong' speed.

b) Create a recursive wave shaping algorithm using delay (i.e. an algorithm in which the output is fed back as input).

Recursive algorithms used to distort sound have technical limits. If you do the following...

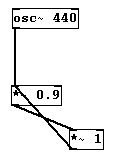
...the error message "DSP loop detected" appears and audio will no longer be sent through the loop. Without using time delay on the signal, you can't create any (audio) recursions.

Here's how you can avoid errors:

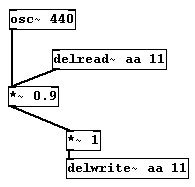
The use of algorithms in musical composition is a broad field. Algorithmic principles can be observed in the work of medieval composers and it has been a widely used area in music since the 20th century. Algorithmic compositions can be fascinating purely from a mathematical perspective. Nature is rich with examples of algorithms. For more information:

http://en.wikipedia.org/wiki/Algorithmic_composition