| Kapitel 3. Audio | ||
|---|---|---|
| | ||
Inhaltsverzeichnis
Von nun an sind die Beispielpatches nicht mehr mit nachträglichen roten Erklärungen kommentiert, sondern mit den regulären Pd-internen Comments (Put Comment), so wie Sie es selbst später auch praktizieren sollten.
Viele der Funktionen, die in Kapitel 2 gezeigt wurden, werden im Folgenden nicht verwendet; das betrifft alle grafischen Elemente und Funktionen wie „send“ und „receive“, obwohl sie freilich in der Praxis immer gebraucht werden. Die hier vorgestellten Patches sind jedoch immer auf das Wesentliche reduziert. Sobald die hier vorgestellten Techniken aber Bestand-TEIL eines Stückes sind, ist es erforderlich, Teile in Subpatches zu packen, sie mit „Inlets“/„Outlets“ zu verbinden etc. Unter Abschnitt 3.4.2.4 wird anhand eines Beispiels gezeigt, wie das aussehen kann.
Fortan sind größere Patches bereits fertig gebaut als extra Dateien vorhanden (http://www.kreidler-net.de/pd/patches/patches.zip).
Erinnern wir uns wieder an unser allererstes Beispiel. Gehen wir dem nach, was wir gehört haben: einen Ton mit 440 Hertz (später auch mit anderen Frequenzen, also anderen Tonhöhen), den wir ein- und ausschalten konnten, das heißt, laut oder unhörbar leise stellen.
Zunächst zur Tonhöhe: In Pd arbeiten wir mit zwei Arten von Tonhöhen – entweder in Hertz oder in MIDI-Zahlen. Die traditionelle Bezeichnung a, b, gis etc. gibt es in Pd gar nicht. Stattdessen haben alle chromatischen Töne MIDI-Nummern, z.B. entspricht a' der Nummer 69, b' 70 etc. Die andere Bestimmung der Tonhöhe erfolgt in Hertz. Um das zu verstehen, müssen wir nun in die Lehre der Akustik eintauchen.
Klang ist Luft, die schwingt. Traditionelle Instrumente sind dazu da, die Luft in bestimmte Schwingungen zu versetzen. Das geht zum Beispiel mit Saiten (Geige), Lippen (Trompete) oder Membranen (Pauke). Auch in unseren Ohren haben wir Membrane, nämlich das Trommelfell, das mit den Schwingungen der Luft mitschwingt. Unser Gehirn transformiert diese Schwingungen dann zu dem, was wir als Klang wahrnehmen.
Bei Elektronischer Musik verwenden wir zur Klangerzeugung Lautsprecher. Diese haben auch eine Membran (oder mehrere), die vor und zurück schwingt und dadurch die Luft zum Schwingen anregt.
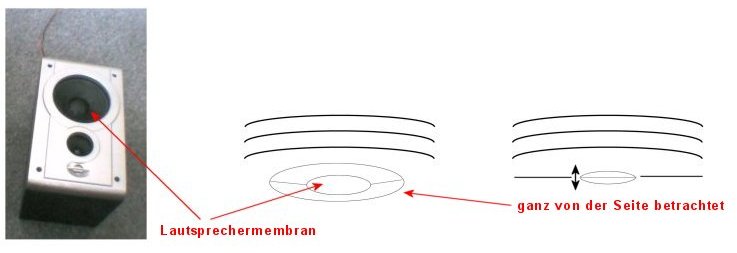
Diese Membran wird jetzt vom Computer aus gesteuert. In Pd übernimmt dies das Objekt „dac~“ (digital audio converter). Damit ist Folgendes gemeint: Klang ist als physikalisches Phänomen, nämlich als Schwingung der Luft, analog. Der Computer selbst arbeitet aber nur mit Zahlen, also digital. Das Objekt „dac~“ macht Zahlen zu Klang, indem es die Zahlen in Stromschwankungen konvertiert, die - entsprechend verstärkt - im Lautsprecher zu Bewegungen der Lautsprechermembran führen.
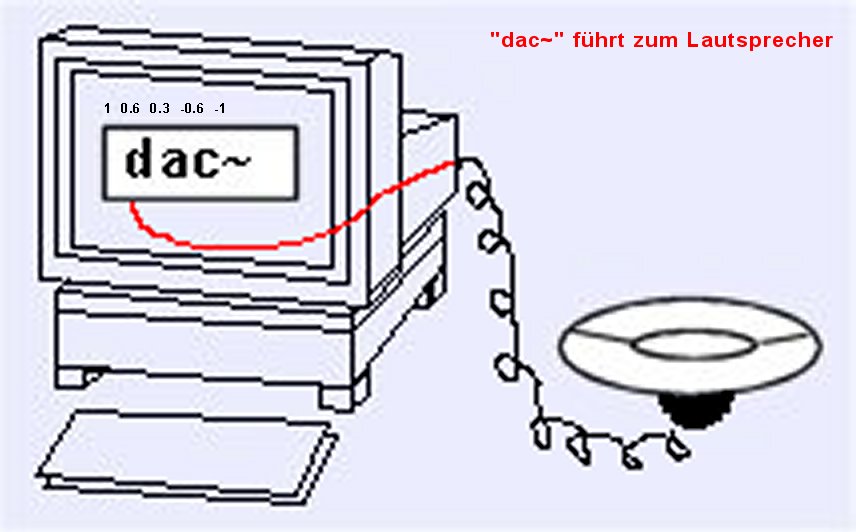 |
Umgekehrt kann man ein Mikrofon an den Computer anschließen. Ein Mikrofon besitzt ebenfalls eine Membran, die durch Luftschwingungen angeregt wird und diese Schwingungen in Form von Stromschwankungen an den Computer weitergibt, der diese Stromschwankungen in Zahlenfolgen umwandelt. In Pd kann dieser Input mit dem Objekt „adc~“ empfangen werden.
 |
Zunächst aber zurück zum Lautsprecher. Dessen Membran kann sich hin- und herbewegen. Die äußerste Position ist für den Computer die Position 1. Die hinterste Position ist für den Computer die Position -1. Wenn die Membran genau in der Mitte, also in Ruhe ist, ist sie in der Position 0. Alle anderen Positionen dazwischen sind Werte zwischen -1 und 1.
 |
In der Realität sind diese Bewegungen so klein und schnell, dass wir sie mit bloßem Auge kaum nachvollziehen können.
Stellen wir uns nun vor, dass sich die Membran immer im gleichen Tempo zwischen den äußeren Grenzen hin- und herbewegt:

Markieren wir nun die einzelnen Stadien:

Abstrahiert, als Schaubild mit y-Achse (Stand der Membran) und x-Achse (Zeit) sieht das dann so aus:


Auf dieser Darstellung sieht man sehr gut die Schwingungsform, ein Dreieck.
So gibt es verschiedene Schwingungsformen, je nach dem, wie die Bewegung der Membran verläuft. Ihre Namen erhält sie von ihrem Aussehen:

Das Pd-Objekt „osc~“ erzeugt eine Sinus-Schwingung.
Das Wichtige bei diesen Schwingungen ist: Sie wiederholen sich dauernd, ohne Änderung ihrer Bewegungscharakteristik. Eine solche Schwingung nennen wir periodisch, da sie periodisch immer wiederkehrt. Eine Periode ist ein vollständiger Verlauf einer Schwingung, der ständig wiederholt wird. Physikalisch spricht man von einer Welle.

Das für uns Besondere an periodischen Schwingungen ist, dass wir solche Schwingungen als Töne mit bestimmten Tonhöhen hören. Dahingegegen sind Geräusche Schwingungen, die unperiodisch sind.

Befassen wir uns aber zunächst nur mit periodischen Schwingungen. Bei ihnen kann man nun zählen, wie oft die Periode in einer Sekunde auftritt. Diese Zahl ist die Frequenz einer Schwingung, ihre Einheit heißt „Hertz“ (Abk. Hz); Frequenz bedeutet immer, wie oft etwas pro Sekunde wiederholt wird (mathematisch ausgedrückt: 1/Sekunde).

Von der Frequenz hängt die Tonhöhe ab. Der Kammerton a' bedeutet, dass die Luft periodisch 440 Mal pro Sekunde schwingt, c'' hingegen 523 Mal pro Sekunde und das tiefe G des Cellos ungefähr 100 Mal pro Sekunde.
Daran sehen wir schon: Je langsamer die Frequenz, desto tiefer der Tonhöheneindruck für unser Ohr. Tatsächlich hört ein Mensch – je nach Alter – Töne zwischen 20Hz und 15000Hz. Kinder können bis zu 20000Hz hören, alte Menschen hingegen oft nur noch bis 10000Hz. Hunde oder Fledermäuse hören noch weit über 20000Hz hinaus. Diesen Bereich nennt man Ultraschall. Im Gegensatz dazu ist Infraschall unterhalb der menschlichen Hörgrenze angesiedelt, also zwischen 0 und 20Hz, Infraschall. Diesen Bereich nehmen wir als Rhythmus wahr. Das kann an diesem Experiment in Pd schön beobachtet werden:

Anfangs hört man einen Rhythmus von Klicks (das ist der Klang eines Sägezahns), der allmählich schneller wird. Ab einer bestimmten Geschwindigkeit (über 20 Klicks pro Sekunde) schlägt die Wahrnehmung in einen Tonhöheneindruck um. Für die Luft (und für den Computer) ist das alles weiterhin immer nur ein „Rhythmus“. Aber für das menschliche Ohr ist es ab einer bestimmten Geschwindigkeit (ca. 20Hz) eine Tonhöhe! Je schneller dieser Rhythmus wird, desto höher die Tonhöhe für uns.
Das Charakteristische für unser menschliches Ohr ist weiterhin, dass wir Tonhöhen logarithmisch hören. Gemeint ist damit: Einer Verdopplung der Frequenz entspricht für unser Ohr der Eindruck eines Oktavsprungs. Wechseln wir von einem Ton mit der Frequenz 440 zu einem mit der Frequenz 880, hören wir zunächst a' und dann a'' :
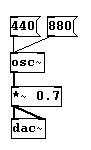
Wollen wir nun aber von 880Hz aus wieder eine Oktav hören, müssen wir +880 nehmen =1760:
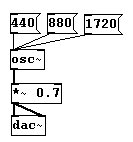
So wird klar: Von 30Hz zu 60Hz hören wir eine Oktav, aber von 1030Hz zu 1060Hz nur einen sehr kleinen Schritt. Tatsächlich ist der Sprung von 10000Hz zu 20000Hz nur der einer Oktav!
Anders, wenn wir zu einer Grundfrequenz immer denselben Betrag hinzuaddieren, z.B zu 100Hz, was ungefähr der G-Saite des Cellos entspricht, zu der wir immer weiter 100Hz addieren:
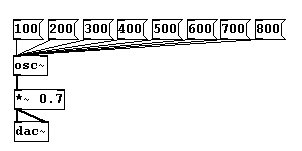
Was wir dann hören, ist von 100 zu 200Hz eine Oktav, von 200 zu 300Hz eine Quint, von 300 zu 400Hz eine Quart etc. Was in Mathematik eine additive Reihe ist, also die Zunahme um immer das gleiche Intervall, ist für unser Ohr eine sukzessive Zunahme um ein immer kleiner werdendes Intervall:
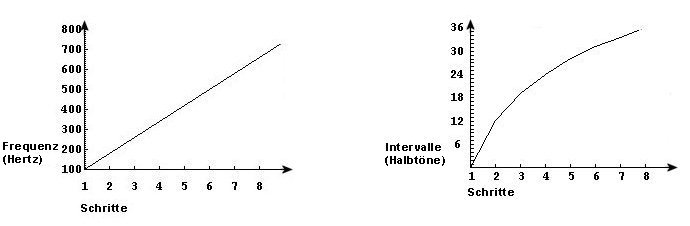
Die linke Darstellung zeigt einen linearen Verlauf – den mathematischen. Die rechte Seite zeigt, was wir hören – einen logarithmischem Verlauf.
Wollen wir umgekehrt einen linearen Verlauf hören – also immer die Zunahme um das selbe Intervall, zum Beispiel der Oktav – müssen wir mathematisch einen exponentiellen Verlauf erstellen:
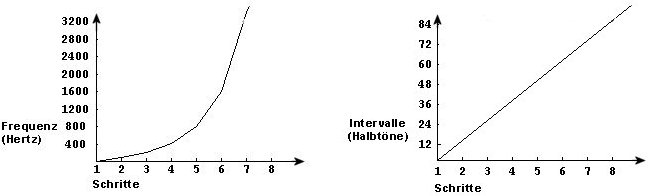
Die Umrechnung von linearem zu logarithmischem Verlauf findet in Pd zwischen MIDI-Nummern und Frequenz statt. MIDI-Nummern entsprechen unserer Hörweise, indem sie für gleich große Schritte immer gleich große Zahlenschritte einsetzen – das ist pro Halbton eine ganze Zahl. Man kann in Pd zwischen Frequenz- und MIDI-Angabe umrechnen:

Eine kleine Tabelle von MIDI-Zahlen, Frequenzzahlen und ihre traditionelle Bezeichnung:
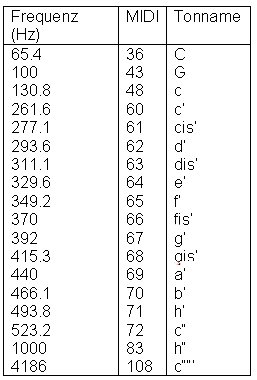
Die regulären Oszillatoren wie „osc~“ oder „phasor~“ müssen als Input jedoch immer Angaben in Hertz erhalten.
Wir müssen uns wieder bewusst machen: Für Pd ist Klang nur Zahlen. D. h., die Membran-Positionen des Lautsprechers sind Zahlen zwischen -1 und 1.
 |
Objekte wie „osc~“ erzeugen eine sehr schnelle Abfolge von Zahlen zwischen -1 und 1, was „dac~“ dann zum Lautsprecher schickt. Genau gesagt werden 44100 Zahlen pro Sekunde erzeugt. Wenn der Lautsprecher sich also in einer Sekunde von -1 zu 1 bewegt, macht er genau genommen 44100 sehr kleine Schritte von -1 hin zu 1. Diese Zahl, 44100, heißt Samplerate.
Jeder Klang in Pd wird durch Zahlen zwischen -1 und 1 erzeugt, und zwar immer in der Geschwindigkeit von 44100 Zahlen pro Sekunde (Samplerate). Eine einzelne dieser Zahlen nennt man Sample.
Alles, was in dieser Geschwindigkeit erzeugt oder bearbeitet werden muss, ist in Pd durch Objekte mit einer Tilde „~“ gekennzeichnet. Untereinander sind diese Objekte mit dicken Kabeln verbunden. Wir nennen diese Zahlenreihen Signale.

Dem Objekt „osc~“ beispielsweise können wir, wann immer wir wollen, eine neue Frequenz-Zahl als Input zuweisen; wir arbeiten damit nicht ständig. Daher eine dünne Verbindung. Aus dem Outlet des „osc~“-Objekts dagegen kommt ununterbrochen Klang, das heißt, Zahlen zwischen -1 und 1, 44100 pro Sekunde (pro Sekunde bedeutet: Hertz).
An den Outlet von „osc~“ können wir keine Number-Box anschließen, um diese Nummern zu sehen. Number-Boxen können nur für Kontroll-Verbindungen verwendet werden, nicht für Signal-Verbindungen. Signal-Verbindungen sind zu schnell, wir könnten 44100 verschiedene Zahlen pro Sekunde gar nicht visuell wahrnehmen. Ausschnitte jedoch können mit dem Objekt „snapshot~“ angezeigt werden. Als Input erhält es den Klang und einen Bang, der, angeklickt, dann den aktuellen Stand ausgibt, zum Beispiel dann zu einer Number-Box oder einem print-Objekt:
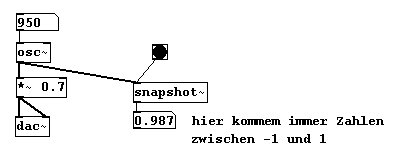
Wollen wir diese dauerhaft sehen, könnten wir ein (schnelles) Metronom anschließen:

In Pd-extended gibt es aber auch „unsig~“, was automatisch ein Metronom anschließt. Als Argument geben wir den Metronom-Wert:

Umgekehrt kann man mit „sig~“ auch Zahlen auf Kontroll-Ebene in Zahlen der Signal-Ebene umwandeln. Oben gibt man nur einmal einen Wert ein, der dann unten 44100 Mal pro Sekunde ausgegeben wird.
Ähnlich wie für die Frequenz (und wie bei der Amplitude im folgenden Kapitel) gibt es also für die Zeitmessung in Pd zwei unterschiedliche Einheiten: Samples und Millisekunden. Samples sind in der Regel die Zählweise bei Signalen, Millisekunden bei Kontrolldaten.
Umrechnung von Millisekunden-Dauern zu Sample-Dauern:

Random-Midi-Werte werden langsam ver-offsettet. (Also: Übergang von temperierter Stimmung zu random-Stimmung):
patches/3-1-1-2-1-random-offset.pd
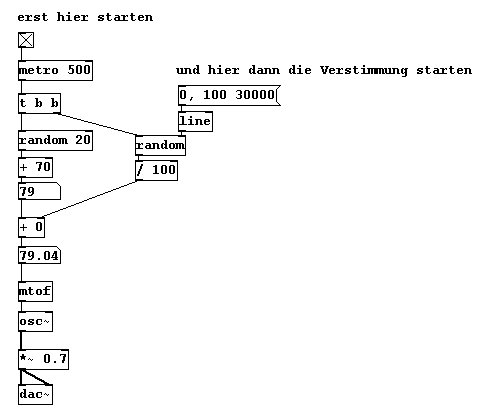 |
Die Zahl 44100 ist mit gutem Grund gewählt. Wie gesagt wurde, hört der Mensch (idealiter) Frequenzen bis zu 20000 Hertz. Der US-amerikanische Physiker Harry Nyquist (1889-1976) stellte 1928 eine Theorie auf, derzufolge man zur digitalen Darstellung eines Signals mindestens die doppelte Signalfrequenz benötigt („Nyquist-Abtasttheorem“). Konkret heißt das, man braucht mindestens die Eckpunkte jeder Periode, um eine Welle in ihrem Grundgerüst darzustellen, also zwei Punkte pro Periode:

Bei einer Welle mit 20000Hz, also mit 20000 Perioden pro Sekunde, brauchen wir mindestens 40000 Punkte pro Sekunde, um sie zu erfassen. Um sicherzustellen, dass dies für alle Wellen innerhalb des menschlichen Wahrnehmungsbereiches möglich ist, hat man entschieden, für Audio-CDs eine Samplerate von 44100Hz zu veranschlagen. Damit kann man also Wellen bis 22050Hz erzeugen. Für Computer existieren jedoch eine große Bandbreite von Frequenzen, die bis 8000 Herz für Systemklänge hinunterreichen. Für hochwertige Audioaufnahmen werden jedoch auch Sampleraten von 48000Hz (bzw. 48 kHz = kiloHertz, für kilo = Tausend) arbeiten, mit 96kHz oder gar mit 192kHz verwendet.
Es ist deutlich geworden, dass die Arbeit mit (vielen) Signalen für den Computer eine große Rechenarbeit darstellt. Man stelle sich nur vor, 100 „osc~“-Objekte zu haben. Jedes einzelne erzeugt 44100 Zahlen pro Sekunde, die miteinander synchronisiert sind. Daher gibt es in Pd die Option, DSP (digital signal processing) im Hauptfenster auszuschalten, wenn es gerade nicht gebraucht wird, um den Prozessor von unnötiger Arbeit zu entlasten.
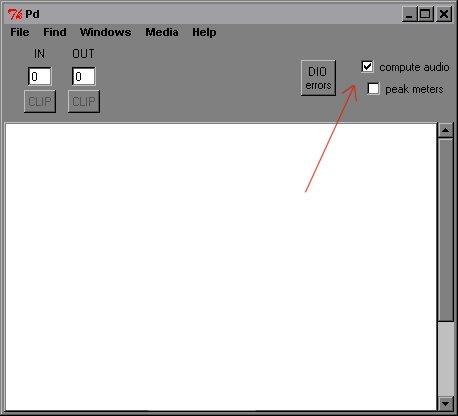
Man kann dies aber auch als Befehl verschicken; der Empfänger „pd“ ist in dem Fall das Programm selbst:

Grundsätzlich gilt für Computermusik, je schneller der Prozessor, desto höher die Leistung.
Pd erleichtert sich die Arbeit, indem es nicht jedes Sample einzeln berechnet und weitergibt, sondern immer eine Menge von Samples abarbeitet und dann als ganzen Block weitergibt. Das optimiert die Leistung wesentlich. Die standard-Blockgröße beträgt 64 Samples, kann aber neu eingestellt werden. Mehr dazu unter 3.8.1.1
Wenn gesagt wurde, der „dac~“ schickt die in Pd erzeugten Zahlen zur Lautsprechermembran (3.1.1.1.1), ist das natürlich verkürzt ausgedrückt. Genau genommen wird in der Soundkarte des Computer aus den Zahlen ein elektrischer Strom mit variabler Spannung erzeugt („digital-analog-Wandlung“, Abk. „da-Wandlung“); je nach Höhe des Spannungswerts liegt dann die Membranposition. Genauso wird umgekehrt im Mikrofon zunächst aus dessen Membranstimmung eine variable Stromspannung gewonnen, die dann in der Soundkarte des Computers digitalisiert wird, d.h., in Zahlen transfomiert.
Schallwellen sind, anders als beispielsweise Wasserwellen, Longitudinalwellen. Longitudinalwellen sind dadurch charakterisiert, dass sie in Bewegunsrichtung des Schalls schwingen und nicht senkrecht dazu, wie Transversalwellen). Für nähere Erläuterungen sei auf das Physikbuch der schulischen Oberstufe verwiesen.
Die Umrechnung von MIDI-Nummer zu Frequenz erfolgt durch „mtof“. Die Formel für die Frequenz f und die MIDI-Nummer m lautet:


Wollen wir einfach die Frequenz eines temperierten Tons wissen, der in einem bestimmten Abstand zu einer bekannten Frequenz steht, benötigen wir diese Formel:
 |
f bezeichnet die gesuchte Frequenz, g die Frequenz des Bezugstons, a den Abstand in Halbtönen.
Möchten wir zum Beispiel die Frequenz von c'' ermitteln und wissen, dass a' die Frequenz 440Hz hat, setzen wir ein:
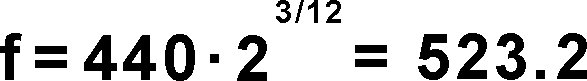 |
In Pd:

Für die umgekehrte Berechnung von Frequenz in MIDI lautet die Formel:
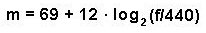
Wobei wir in Pd nur den natürlich Logarithmus auf Basis der Euler'schen Konstante haben; daher brauchen wir noch diese Formel:

Somit in Pd:

Es wurde gesagt, dass Geräusche keine Periode haben. Nun könnte man sich aber vorstellen, dass ein Rauschen zehn Sekunden läuft und dann in einer exakt gleichen Schleife wiederholt wird – dann hätte das Rauschen theoretisch doch eine periodische Frequenz, nämlich von 0.1Hz. Darum lautet die Definition für ein Geräusch genauer, dass es unperiodisch ist oder eine Periode von weniger als 20Hz hat. Entsprechend kann auch gesagt werden: Die Frequenzen von Geräuschen haben evtl. einen gemeinsamen Grundton, nur eben unterhalb von 20Hz.
Das Gebiet der Akustik birgt lauter spannende Experimente, etwa in Form der Längenberechnung von Schallwellen oder des Dopplereffekts. An dieser Stelle sei ausdrücklich auf die Lektüre einschlägiger Akustiklehrbücher verwiesen.
Die nächste Eigenschaft eines Tons, die wir betrachten wollen, ist seine Lautstärke. Traditionell wird Lautstärke in Musik mit Anweisungen wie pianissimo, piano, mezzoforte etc. notiert. Ihre Verwendung ist allerdings subjektiv und je nach Instrument mitunter sehr verschieden. In der Physik, und danach richtet sich Pd, wird Lautstärke objektiviert mit deziBel- oder root-mean-square-Werten. Die beiden sind vergleichbar mit MIDI-Nummern und der Frequenz-Angabe für Tonhöhe. deziBel (Abk. dB) richtet sich linear nach unserem persönlichen Höreindruck, wobei quasi eine Oktav in Lautstärke dem Intervall von 6dB entspricht. Insgesamt rangiert die Skala von 0 bis 130 dB – wobei absolute Stille immer noch einen Wert von zwischen 15 und 20 dB hat und Schall von über 120dB Lautstärke gesundheitsschädlich ist. Ab 130dB nehmen wir Schall praktisch nur noch als Schmerz wahr. root-mean-square-Werte (Abk. rms) entsprechen wie bei Frequenz-Werten nicht unserem Höreindruck, sondern verlaufen logarithmisch von 0 bis 1. 0 entspricht dabei 0dB, 1 entspricht 100dB. Unter rms versteht man den geometrischen Mittelwert, der aus einer Folge von Amplitudenwerten errechnet wird. Hierzu werden die Zahlen zunächst quadriert, dann der Mittelwert gebildet (duch Summation und Division durch die Anzahl der Elemente) und anschließend aus dem Mittelwert die Wurzel gezogen. Bei einem Audiosignal wird der rms-Wert über einen zeitlich begrenzten Ausschnit des Signals ermittelt und gibt bei einem stark schwankenden Signal, wie einer Schwingung, einen Anhaltspunkt über die ungefähre durchschnittliche Amplitude des Signals in diesem Ausschnitt. Für die Umrechnung vom einen ins andere gibt es folgende Objekte in Pd:

Die Lautstärke einer Schwingung bestimmt sich aus ihrer Amplitude. Das ist der Grad der Auslenkung der Membran über den Nullpunkt hinaus nach vorne und hinten. Je stärker sich die Membran bewegt, desto lauter nehmen wir den Klang wahr. In unserer Achsendarstellung sieht das so aus:
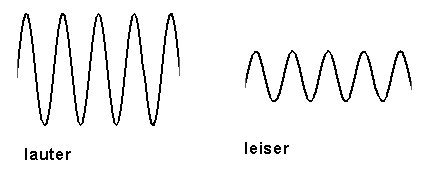
Es muss immer wieder betont werden: Bis dies mit dem „dac~“-Objekt an den Lautsprecher geschickt wird, arbeitet Pd nur mit Zahlen. Wenn also ein Klang leiser ist, heißt das, die Zahlen werden nicht mehr zwischen -1 und 1 produziert, sondern in kleinerem Ambitus um den Nullpunkt herum, zum Beispiel nur zwischen -0.5 und 0.5. Wir bewerkstelligen dies im Patch, indem wir die vom „osc~“-Objekt produzierten Zahlen mit einem Faktor versehen:

So können wir alle Grade von Lautstärke einstellen, von absoluter Stille bis zur größten Lautstärke (letztere hängt natürlich noch von den vorhandenen Lautsprechern und dem Verstärker ab).

Nun könnte man auch eine Art Schieberegler anbringen, und zwar mit dem HSlider (Put HSlider), den man auf einen Bereich zwischen 0 und 1 einstellt (vgl. Kapitel 2.2.2.3.2 und 2.2.4.3.4):

Spätestens wenn man diesen Slider schnell bewegt, kommen nun aber Störgeräusche auf. Das liegt daran, dass ein Signal, das in Samples gerechnet wird, in Konfrontation mit einer Kontrolldaten-Bearbeitung (die in Millisekunden abläuft) gerät. Wenn es nur um vereinzelte Zahlen geht wie zuvor bei den Faktoren 0, 0.1, 0.4, 0.7, 1, ist das irrelevant; ab einer bestimmten Geschwindigkeit spielt es allerdings sehr wohl eine Rolle. Darum muss man die Kontrolldatenverbindung dann durch ein Signal-Pendant ersetzen. Wir konvertieren mit dem „sig~“-Objekt:

Damit ist nun Synchronität zwischen der Zahlenproduktion des Oszillators (44100 Zahlen pro Sekunde) und der Eingabe des Faktors („sig~“ macht daraus ebenfalls genau 44100 Zahlen pro Sekunde) hergestellt. Es gilt noch zu beachten: Kommt in den rechten Inlet von „*~“ ein Signal, darf als Argument nichts in dem Objekt stehen; stünde darin ein Argument (wie vorhin 0.5), ginge das Objekt davon aus, dass es rechts einen Kontrolldaten-Input erhielte.
Um ein Crescendo oder Decrescendo zu erstellen, müssen wir entsprechend „line~“ verwenden:

Eine elegantere Verwendung des Sliders als Lautstärke-Schieberegler („Potentiometer“) wäre folgende:

So wird noch zwischen jedem Schritt ein kleines Crescendo / Decrescendo durchgeführt. Diese Auffüllung von Schritten mit Zwischenwerten nennt sich „Interpolation“ (wie schon mit Tonhöhen in Kapitel 2.2.3.2.3 geschehen).
Wir können die Lautstärke eines Tons mit dem Objekt „env~“ ermitteln, das die Lautstärke in dB ausgibt. Es muss immer ein Zeitraum definiert werden, innerhalb dessen ein Durchschnittswert gebildet wird; wir geben ihn als Argument in Samples an (üblicherweise als Sample-Zahl eine 2er-Potenz):

Mit der Umrechnung in rms ...

... sieht man, dass die Faktoren zwischen 0 und 1 nicht zu verwechseln sind mit rms-Werten zwischen 0 und 1.
Wie schon angedeutet, entspricht das menschliche Hören bei der Lautstärke wie bei Tonhöhe nicht den Ergebnissen der physikalischen Messung (wie in der Gegenüberstellung der Schaubilder für Tonhöhen in Frequenzen und Intervallen). Ein einfacher Trick, um einen lineareren Eindruck einer Lautstärkezunahme oder -abnahme zu erzielen, ist es, die Werte zu quadrieren:

Hier sind aber alle möglichen Verläufe auszuprobieren; letztlich ist es eine kompositorische Entscheidung, wie die Lautstärke zu- oder abnehmen soll. Was denn eine „Lautstärken-Oktav“ sei, kann nicht so objektiviert werden wie bei Tonhöhen.
Zur Visualisierung der Amplitude gibt es in Pd ein eigenes GUI-Objekt: Den VU-Meter (Put VU). Als Input erhält er eine dB-Angabe. Allerdings ist er so konstruiert, wie Anzeigen auf herkömmlichen Mischpulten eingestellt sind: 100dB werden als 0dB angezeigt und Abweichungen davon gehen dann in den Minus- oder Plus-Bereich. Dies muss so bereits als Input gegeben werden. Also einfach vom Output von „env~“ 100 subtrahieren:

Dann zeigt der VU Lautstärkeänderungen grafisch an. (VU ist die Abk. für „Volume“ = engl. für Lautstärke).
In Pd-extended gibt es zur Konversion für den VU-Meter auch das Objekt „pvu~“:
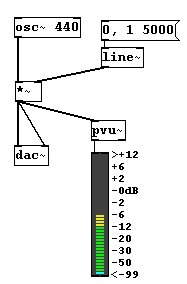
Wichtig ist noch: Amplituden über 1 und unter -1 werden 'abgeschnitten'. Erhält der Lautsprecher vom „dac~“ einen Wert jenseits von 1 oder -1, bleibt die Membran an der äußersten Stelle einfach stehen.

Erhöht man die Lautstärke eines Klanges derart, dass der Verlauf seiner Schwingung durch das Stehenbleiben der Membran 'abgeschnitten' wird, entsteht der Effekt, den man Übersteuerung nennt.

Eine weitere Widrigkeit ist folgende: Wird die Position der Lautsprechermembran ruckartig um ein größeres Intervall versetzt (wenn man zum Beispiel den Klang einschaltet), erklingt ein sogenannter „Klick“:
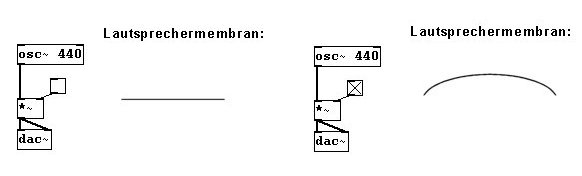
Dies tritt jedoch nur dann stark in Erscheinung, wenn als eigentlicher Klang eine Schwingung verwendet wird, die selbst eine sehr geschmeidige Membranbewegung erzeugt, also z.B. der Sinuston. Im Schaubild ist der „Ruck“ gut zu erkennen:

Ein „Ruck“ bedeutet in der Regel eine Versetzung, die schneller als 30ms ist. Um solche Klänge ohne Klick einzuschalten, sollte man daher eine sogenannte „Rampe“ bauen, d.h. ein sehr schnelles Crescendo am Anfang und am Ende erzeugen:
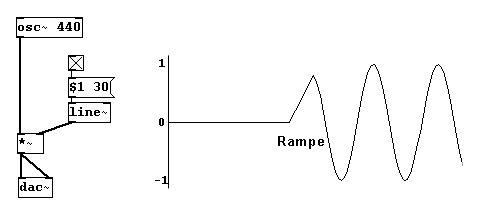
Außerdem lässt sich an der Welle eines Klangs in Pd einstellen, bei welcher Membranposition er beginnen soll (oder wo er hinspringen soll). Dies nennt man die Phase einer Welle. Man kann die Phase in Pd im rechten Inlet des „osc~“-Objekts einstellen, mit Zahlen zwischen 0 und 1:

Die gesamte Periode einer Welle wird also wieder eingefasst in den Bereich zwischen 0 und 1. Häufig wird sie aber auch in Grad benannt, wobei die komplette Periode 360 Grad hat. Zum Beispiel ist häufig die Rede von einer „Phasenverschiebung um 90 Grad“. Dem entspricht in Pd ein Input für die Phase von 0.25.
Die Änderung der Phase einer Welle hat zunächst für unser Ohr keine besondere Auswirkung. In anderen Zusammenhängen werden auf die Phasenlage allerdings zurückkommen.
Hat man diese beiden Oszillatoren:
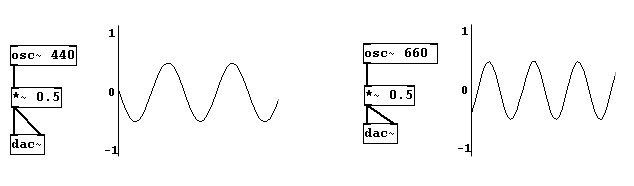
... und schließt sie zusammen an den „dac~“, ergibt sich Folgendes:
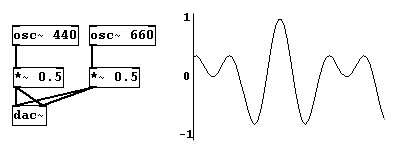
Die beiden einzelnen Wellen gingen (wegen des Faktors) nur von -0.5 bis 0.5. Zusammen aber reichen sie nun von -1 bis 1 und bilden eine etwas komplexere Form. Das liegt daran, dass sich Schallwellen grundsätzlich addieren. Einfach gesagt: Wie haben nur eine Luft, die alle Schwingungen, die ausgelöst werden, gleichzeitig vollziehen muss. Addition heißt aber auch, dass es zu Auslöschungen kommen kann. Gegenläufige Wellen, bei denen die eine immer gerade „nach hinten“ geht, während die andere „nach vorne“ geht, gleichen einander aus. Das ist der Fall, wenn gleich schnelle Schwingungen in Gegenphase sind:
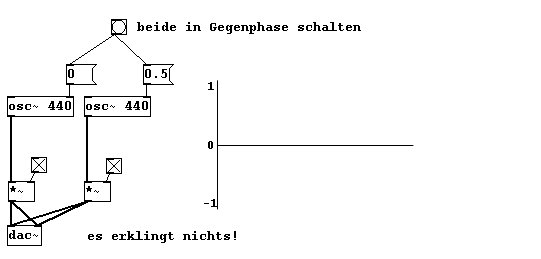
Normalerweise müssen wir aber bei Beteiligung mehrerer Klangproduzenten an einem Gesamtklang die Summe so heruntermultiplizieren, dass sie einen Wert von 1 bzw. -1 nicht über- bzw. unterschreitet:
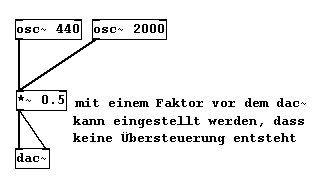
Hier werden einfach beide Oszillatoren an ein Multiplikationsobjekt angeschlossen. Dadurch werden sie zunächst automatisch addiert (wenn immer mehrere Signale als Input eines einzelnen Objekts gegeben werden, werden sie zunächst addiert und dann gemäß dem Objekt bearbeitet), und dann der Multiplikation unterzogen.
Wir erstellen einen Akkord mit variabler Lautstärke für jeden einzelnen Ton:
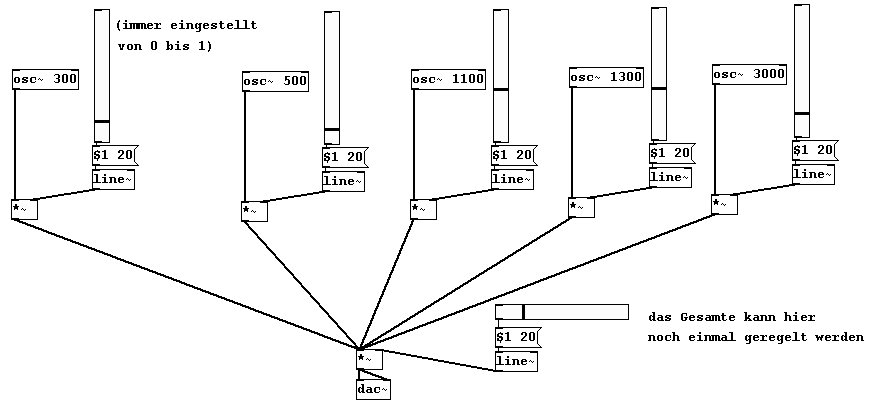
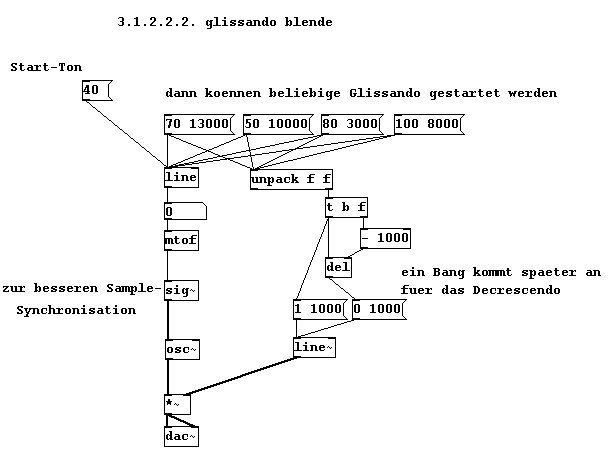
Glissandi, die am Anfang und Ende geschmeidig ein- bzw. ausblenden:
patches/3-1-2-2-2-glissandi-blende.pd
Nehmen wir ein Mikrofon, sprechen etwas hinein und geben dies mit veränderter Lautstärke wieder aus:
patches/3-1-2-2-3-input-bearbeiten.pd

Werden wir 'symphonisch': Warum nicht gleich zwanzig verschiedene Oszillatoren etwas spielen lassen?
patches/3-1-2-2-4-oszillatorenkonzert1.pd
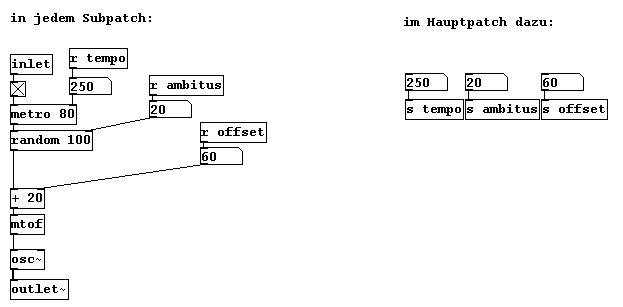
Erstellen wir zunächst diesen Subpatch „o1“:

... und vervielfältigen ihn dann einige Male

Nun schalten wir alle nacheinander ein!
Hier sei nur angedeutet, dass sich nun natürlich alle Parameter ändern lassen – und schon hat man etwas zum Spielen:
patches/3-1-2-2-4-oszillatorenkonzert2.pd
Schall bewegt sich in der Luft bei 20 Grad Celsius mit ca. 343 Metern pro Sekunde. Wir können nun die räumliche Länge einer Periode berechnen und das Ergebnis auch gleich überprüfen ...
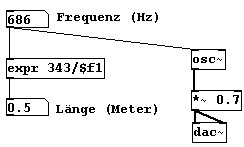
... indem wir zum Beispiel bei einer Frequenz von 686 Hertz unseren Kopf einen halben Meter weit hin und her bewegen, hören wir deutlich Wellenberg und Wellental.
a) Erstellen Sie (random-)Glissando-Akkorde, zusätzlich noch mit einer random-Lautstärkeänderung für jeden einzelnen Ton.
b) Die Lautstärke des Mikrofoneingangs soll die Tonhöhe eines Oszillators steuern (dann auch mehrere mit jeweils verschiedenem Frequenz-Offset)!
Von einigen Objekten, die wir in Kapitel 2 kennengelernt haben, gibt es auch eine Version mit Tilde. Sie funktionieren genau gleich, nur dass sie eben Signale statt Kontrolldaten verarbeiten:
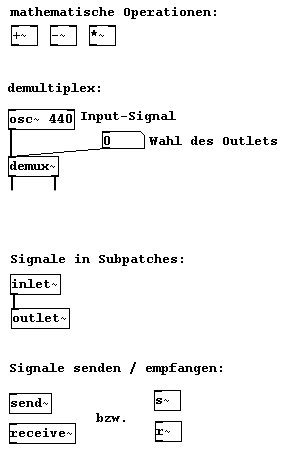
Mit „send~“ kann etwas an beliebig viele „receive~“-Objekte geschickt werden; umgekehrt darf es aber nur ein „send~“-Objekt sein:
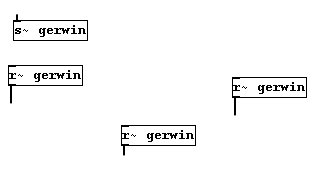
Umgekehrt kann man viele verschiedene Signale an eine zentrale Stelle leiten (eben zum Beispiel zum „dac~“), mit „throw~“ und „catch~“:

Relevant für Pd ist ferner die Bit-Tiefe. Der Prozessor eines Computers arbeitet nur mit dem binären Zahlencode, d.h. mit 0 und 1. Die Bit-Anzahl besagt, wieviele Plätze für Nullen und Einsen verwendet werden. Hätte man z.B. nur zwei Stellen, könnte man nur 22, also vier verschiedene Kombinationen erstellen:
0 0
0 1
1 1
1 0
Je mehr Stellen man hat, desto mehr bzw. detaillierter kann etwas verarbeitet werden. Für Pd, wo ja Erscheinungen wie Frequenzen, Amplitude etc. mit Zahlen berechnet werden, bedeutet dies, dass diese Zahlen je nach Bit-Tiefe genauer berechnet werden können – die Anzahl der Kommastellen hängt also davon ab. Pd arbeitet normalerweise mit 16 Bit, das entspricht der Qualität einer Audio-CD. 16 Bit entspricht 216 = 65,536 möglichen Werten für ein Sample.
Lautstärke und vor allem Lautstärke-Intervalle sind objektiv wie subjektiv sehr abhängig, z.B. von den Charakteristika des Raumes, vom Lebensalter des Hörers etc. Es gibt auch nicht eine einzige präzise Messung für Lautstärke; bekannt sind die Theorien von Schalldruck und Schallintensität. Ergänzend hierzu sei ausdrücklich der Blick in ein Buch über Akustik empfohlen.
Wir haben nun gesehen, dass es für die wesentlichen Bereiche der Klangerzeugung in Pd jeweils zwei verschiedene Einheiten gibt: für die Tonhöhe Frequenz und MIDI-Nummern, für die Amplitude root-mean-square und deziBel und für die Zeit Millisekunden und Samples.
Für Letzteres soll noch das weiter oben angeführte Beispiel mit Crescendo/Decrescendo von „line~“ erläutert werden:
Würde man „line“ (ohne Tilde) hierzu einsetzen, kann es zu unerwünschten Knacksern oder Ähnlichem kommen, da die beiden Zeitmaße kombiniert werden; das Problem ist, dass sie nicht synchronisiert sind. Es kann passieren, dass die Zahlenschritte nicht zusammentreffen und dadurch Unregelmäßigkeiten verursachen, die sich durch kurze Verzögerungen oder eben Knackser äußern.
Wie in Kapitel 2.2.3.3.2 beschrieben wurde, gibt „line“ alle 20 Millisekunden einen Wert. Das heißt, es trifft möglicherweise nicht mit dem Sample-Aufkommen zusammen. Zwar kommt ca. alle 0.02 Millisekunden ein neues Sample, dennoch kann ein „line“-Wert gerade nicht mit einem mehr oder weniger gleichzeitigen Sample zusammentreffen und dann kommt es zu Komplikationen. „line~“ (mit Tilde) hingegen erzeugt ein Signal mit 44100 Werten pro Sekunde; diese 44100 Werte werden exakt zeitgleich generiert wie sie irgendein anderes Tilde-Objekt erzeugt; sie sind immer synchron. Der Computer arbeitet grundsätzlich 44100 Samples pro Sekunde ab und an verschiedenen Orten im Patch immer genau zeitgleich.